GALARTMATH : recherche, découverte et exploration de nouveaux mondes graphiques
Présentation de la démarche artistique
Précision importante
Dans cette section, je présente toutes les étapes de recherche et de création par lesquelles je suis passé. Ce qui signifie que je présente des images ” du début à nos jours ” Il y a donc des images qui m’ont plu à un moment particulier et qui, le travail de recherche progressant, me plaisent moins aujourd’hui. Je les conserve néanmoins car elle font partie de mon parcours. Il s’agit donc d’une présentation historique.
Démarche artistique : première version
Mon travail artistique est alimenté par trois sources :
- L’éducation artistique que j’ai reçue,
- Les mathématiques,
- L’informatique.
Je suis né, en effet, dans une famille qui aimait l’art sous toutes ses formes : architecture civile, militaire et religieuse, peinture, sculpture, arts décoratifs…
Durant ces années de jeunesse, j’ai également beaucoup dessiné ; du figuratif mais surtout de l’abstrait. J’ai laissé derrière moi une multitude de dessins dont la plupart sont perdus.
Le choc fut la découverte de l’encre de Chine que j’ai eu à utiliser au cours de mes études scientifiques. Sa découverte a été une espèce de révélation et très vite je m’en suis servi pour dessiner essentiellement de l’abstrait. Ceci m’a donc orienté à travailler sur le trait.
Ainsi pendant mon enfance et ma jeunesse, j’ai toujours baigné dans un environnement où les Arts avaient une très grande place. Et ceci perdure à l’âge adulte. Mon goût pour les arts visuels m’accompagne ainsi depuis mon enfance.
Enfin, j’ai étudié les mathématiques et j’ai appris à me servir d’un ordinateur pour devenir ingénieur mathématicien.
Une précision importante et déterminante dans ma « démarche numérique » est que, pour réaliser de telles images, je me suis fixé trois contraintes :
- créer des images uniquement à l’aide de formules et de transformations mathématiques,
- ne pas utiliser des techniques existantes dont j’ai connaissance comme par exemple les fractales,
- ne pas rendre perceptible la nature mathématique et calculatoire des images.
Ces trois contraintes impliquent qu’il faut rechercher des formules mathématiques qui n’existent pas « sur étagère » : je suis donc parti de la feuille blanche ou bien de l’écran noir.
Précision : je ne me sers d’aucun logiciel de création/traitement d’images tel que Photoshop par exemple. Je n’utilise qu’un langage de programmation « basique » qui me permet de programmer les formules donnant la position de chaque point dans l’image. Tout ce que je fais est conçu et réalisé de cette manière.
C’est notamment cet aspect qui rend mon travail original dans le domaine des « arts numériques » Je n’ai pas en effet trouvé des artistes qui créent leurs œuvres de cette manière.
POUR MIEUX COMPRENDRE MON TRAVAIL je vous invite à aller voir les images que je vous présente et revenir ici pour de plus amples informations.
Présentation détaillée
Les images sont toutes construites à partir de points reliés les uns aux autres par un trait. Les positions des points de l’image sont calculées à partir de « formules mathématiques » que j’invente. Pour créer l’image finale je joue sur la nature des traits : épaisseur, couleur, transparence etc.
Originalité de la démarche
Je ne « peins » pas c’est-à-dire que je ne décide pas a priori de peindre un bouquet de fleur par exemple. Les « formules mathématiques » que j’invente ont un comportement imprévisible tant elles sont complexes quoique non aléatoires. Bien sûr je finis par en « apprivoiser » certaines mais cela ne peut se produire qu’en expérimentant encore et encore c’est-à-dire en jouant sur telle ou telle partie des équations ou en changeant la valeur de certains paramètres. Je travaille sur les traits et leurs caractéristiques : couleurs, épaisseurs, transparence etc. La mise au point est longue ; elle peut durer des semaines ou des mois. Parfois, donc a posteriori, l’image obtenue peut faire songer à « quelque chose » et il est intéressant de recueillir la perception des personnes qui regardent.
Processus de création des images
On peut décomposer mon travail en trois phases :
Phase 1 : recherche
Il s’agit d’une phase d’expérimentation durant laquelle je programme des formules permettant d’aboutir à une image primitive. Cette phase est longue car il faut beaucoup d’essais et d’allers-retours sur les formules pour tenter de trouver les « bonnes » c’est-à-dire celles pouvant aboutir à des images qui me plaisent ou qui peuvent a priori donner des images intéressantes d’un point de vue esthétique.
Phase 2 : découverte
A partir des résultats de la première phase, je ne travaille plus sur la structure des formules mais sur des premiers réglages me permettant d’en estimer le potentiel esthétique. Au terme de cette phase j’aboutis, dans le meilleur des cas, à quelques variantes prometteuses.
Phase 3 : exploration
Il s’agit de la phase de recherche des réglages fins la plus exhaustive possible me permettant d’obtenir des images qui me conviennent. C’est surtout dans cette phase que s’exprime la créativité artistique.
Nature des images
Les images sont constituées de points et de traits. Quand, sur l’écran de mon ordinateur j’aboutis à un « dessin » qui me plait je génère le fichier JPEG correspondant. Ce fichier est d’un type équivalent à celui des fichiers des images que l’on prend, par exemple, avec son smartphone. On peut ainsi agrandir ou réduire la taille de l’image finale. J’ai recours à l’impression dans des situations bien spécifiques… Par exemple lors d’une exposition à thème dans une exposition collective.
Impression
Une fois encore elle peut se faire de différentes manières
- Papier photographique de grammage élevé (de 220 à 300g/m² par exemple) en graphique brillant, satiné ou mat.
- Impression sous acrylique avec Dibond en aluminium et châssis rentrant
- Impression Subligraphie®. Il s’agit d’une impression sur plaque d’aluminium recouverte d’un vernis spécial qui permet d’obtenir l’image en chauffant plus ou moins la plaque pour obtenir fidèlement les couleurs. L’effet visuel s’apparente peu ou prou à l’impression sous plaque acrylique. Cette technique produit des tirages moins fragiles et plus légers que l’acrylique.
Les images que je vous présentent sont le fruit d’une dizaine d’années de travail ; entrecoupées bien sûr de périodes de « maturation »
Et je continue à rechercher de nouvelles images. Je ne comprends pas, en effet, qu’un artiste puisse continuer à publier peu ou prou la même œuvre. Je cherche à « bouger » c’est-à-dire à produire de nouveaux « types » d’images. Le travail étant long et complexe je n’en publie que peu.
Les images sont très variées. Les deux premières sélections d’images que vous trouverez vous en donnent un aperçu (non exhaustif). Les suivantes vous présentent une sélection d’images que j’ai réalisées et que je vous soumets.
Vous trouverez d’autres œuvres et des informations complémentaires sur ma page Facebook https://www.facebook.com/Galartmath .
Conception des images
Afin d’éviter des redites, je vous propose de présenter les étapes qui sont communes à toutes les créations d’images.
Pour créer une nouvelle image je choisis arbitrairement de travailler sur une image en nuances de gris ou bien en couleurs. Pourquoi ? Je n’en sais rien. J’ai simplement envie d’en faire une. La plupart du temps je pars d’une image primitive en noire et blanc que j’avais obtenue il y a plusieurs mois ou bien souvent plusieurs années. Ensuite je commence à la faire “bouger” en travaillant sur les formes, le trait et son épaisseur, sa couleur… Cette façon de procéder prend beaucoup de temps d’expérimentation et de réglage mais ce travail est incontournable.
Remarque. Ces travaux bénéficient des résultats des expérimentations passées ce qui peut faire croitre le nombre d’images qui me conviennent ou bien aboutir à un nouveau « type » d’images.
En complément, je vous propose d’aller au paragraphe « Originalité de la démarche » de la présentation artistique.
Démarche artistique : seconde version
Je crée des images de façon expérimentale.
Ces images peuvent être monochromes : dans ce site ce type d’images est présenté en noir bien que le noir ne soit pas une couleur à proprement parlé sauf quand Soulages le travaille. Elles peuvent également être polychromes (ocre, bleu, rouge…) ou colorées avec des nuances d’une couleur particulière par exemple le bleu comme pour l’image ci-dessous.
Ces images peuvent apparaître comme étant « purement » abstraites mais elles peuvent également faire songer – parfois de manière évidente – à des fleurs, des insectes, des objets… Mais cet aspect figuratif n’est pas ce que je recherche le plus et, dans mon travail, cela est plutôt anecdotique mais parfois assez amusant. Vous en trouverez quelques exemples sous l’onglet « Images monochromes »
flk
Le tondo bleu-1 – The blue tondo 1- FLK – 2016
![]()
Comme l’œil qui regarde veut pratiquement toujours donner une espèce de « sens » à ce qu’il voit, je ne voulais pas initialement risquer d’influencer la perception de qui regarde en donnant un ” titre ” aux images.
C’était ma démarche initiale mais beaucoup de personnes m’ont cependant conseillé de le faire. Lors d’une exposition, où j’ai présenté une sélection de 15 images, j’ai eu la surprise de constater que ce que je croyais être évident (il s’agit du ” Bouquet rouge ” sous l’onglet ” Images monochromes “) ne l’était pas du tout car la personne en question ne voyait pas un bouquet mais… des personnages! Par conséquent nommer les images peut être intéressant notamment si en retour la personne qui la voit la nommerait différemment. Les noms que je donne peuvent traduire la vision que j’ai de l’image ou l’émotion qu’elle me procure. Je ne m’interdis pas toutefois d’y mettre parfois une pointe d’humour teintée d’absurdité ou de donner des titres volontairement abscons à certaines images. Cependant, et en procédant de cette manière, il reste des images ” sans nom ” et cela me convient …
Je tire ou fais tirer les images par un imprimeur (pour plus de détail suivez ce lien) et, en fonction de l’image, j’ai fait le choix d’un papier brillant pour, par exemple, avoir des images contrastées avec des bords bien nets.
Une précision qui me parait être importante : hormis la couleur que l’on peut librement choisir, toutes les images que je présente sur ce site ont été obtenues uniquement par calcul.
On peut parfaitement ne pas avoir de connaissances mathématiques particulières mais se dire ” les mathématiques peuvent donner cela? ” et si en plus vous trouvez mes images esthétiquement intéressantes alors la preuve serait apportée que les mathématiques peuvent être source d’étonnement, de rêveries, d’émotion voire de beauté.
Voici le principe de création des images.
On peut créer des « images » de multiples façons avec des pinceaux (huile, acrylique, etc.), des crayons, des pastels, des roches (lithographie), du métal (gravure…) et bien d’autres moyens (photographie par exemple) Les supports peuvent être très variés toile, papier, métal, murs, verre etc. L’artiste utilise alors ces outils pour créer son œuvre sur le support qu’il a choisi.
Pour reprendre l’exemple de la photographie, les images que vous prenez sont faites, dans la plupart des cas, à l’aide d’un appareil photo numérique comme, par exemple, celui de votre smartphone. L’image est alors une « image » numérique c’est-à-dire un fichier de nombres. Ce fichier est constitué d’une succession de points (les pixels) décrits au moins par leur position et leur couleur. Le fichier numérique peut être « travaillé » à l’aide d’outils de traitement d’images plus ou moins complexes pour, par exemple, supprimer ou atténuer les yeux rouges d’un portrait. Ces outils sont des programmes informatiques fonctionnant à l’aide du processeur de votre smartphone. On peut également transférer ces images sur un ordinateur et utiliser des outils de traitement d’images plus sophistiqués (Photoshop par exemple)
Je suis exactement cette façon de faire mais avec d’autres outils. Pour créer mes images, les outils que j’utilise sont un ordinateur qui, à l’aide des équations et des transformations que j’imagine, permet de créer une image numérique dont les points sont obtenus par calcul. Pour travailler, mettre au point ou créer de nouvelles images j’ai développé plus de 300 outils informatiques. Les images sont visualisées sur un écran.
Et, la plupart du temps après de multiples essais, j’aboutis – parfois – à une image qui me plait et que j’imprime ou fait imprimer actuellement sur papier photographique brillant.
Mon travail peut donc être rattaché à la mouvance des arts numériques.
Pour une première visite je vous conseille d’aller voir des images un peu partout sur le site et en particulier les pages suivantes :
Singularités et surtout la page Publications qui présente les nouveautés.
et revenir ici pour prendre connaissance de quelques éléments supplémentaires sur la démarche qui est la mienne.
Enfin, suivez le lien Informations pratiques pour avoir des informations sur les couleurs, les dimensions, l’encadrement etc.
La technique que j’emploie offre beaucoup de liberté ce qui permet d’obtenir des images UNIQUES qui peuvent être les vôtres.
Si vous avez des demandes particulières, le mieux est donc de me contacter (voir page “contact“)
![]()

GALARTMATH : recherche, découverte et exploration de nouveaux mondes graphiques
Démarche artistique: présentation plus approfondie
Je présente ici mon parcours et donne des complément sur la création des images.
Il s’agit en quelque sorte de “mon histoire”
ici flk
Sommaire
FLK
Petit billet d’humeur en guise d’introduction
Lorsque je parle d’équations, de calcul etc. beaucoup de personnes ont l’esprit qui se fige. De mon point de vue, ceci leur rappelle les heures douloureuses pendant lesquelles des professeurs étaient censés enseigner les sciences mathématique et physique. Ayant enseigné moi-même pendant plus de dix ans, j’ai été confronté à ce problème: pourquoi ce que je disais n’était pas ou mal compris?
La réponse ” classique ” et au demeurant stupide, est de dire ” y’a les matheux et y’a des lettreux ” .
Non.
Il y a certes des esprits qui auront des préférences et/ou des facilités pour apprendre telle ou telle matière, mais il est absolument anormal que l’enseignement des mathématiques soit aussi catastrophique. Il ne s’agit pas de faire des ” génies ” – c’est également le cas pour toutes les autres disciplines – mais d’enseigner quelques notions sur cette partie du savoir et du génie humain. Si on se pose la question classique ” mais les maths à quoi ça sert? ” on peut répondre ” en creux ” en disant par exemple que sans les mathématiques nous n’aurions pas le GPS. Ce serait également le cas s’il n’y pas la physique et en particulier la théorie de la relativité générale qui s’appuient grandement sur les mathématiques.
L’échec de l’enseignement des mathématiques ” classiques ” étant patent est donc inacceptable.
Il serait salutaire que l’enseignement des mathématiques (collège puis lycée) soit remis à plat et surtout que la pédagogie soit enseignée aux enseignants :
la pédagogie cela s’apprend!
FLK
Les débuts : contexte et objectifs
Ayant étudié les mathématiques ou plus exactement essayé d’en comprendre une – petite – partie, j’ai toujours pensé, bien que l’idée ne soit pas neuve, que l’on pouvait créer des images en utilisant :
- Les mathématiques (de base évidemment)
- Un langage de programmation,
- Un calculateur,
- Et un écran permettant de visualiser les résultats.
Pour réaliser de telles images “mathématiques”, je me suis fixé de plus trois contraintes :
- La première : créer des images uniquement à l’aide d’équations ou de transformations mathématiques,
- La seconde : ne pas utiliser les techniques existantes dont j’ai connaissance comme par exemple les fractales,
- La troisième : ne pas voir la nature mathématique et calculatoire des images et c’est cela qui constitue la véritable difficulté à surmonter et qui est au cœur de ce que je fais.
Ce troisième point est très important car il signifie, entre autres, que je ne suis pas à la recherche de je ne sais quelle prouesse ou performance mathématique, comme par exemple réaliser des images d’objets mathématiques complexes. Je cherche seulement à faire des images, si possible d’un genre nouveau et pouvant présenter, de mon point du vue, un intérêt artistique et c’est tout. Et ce n’est déjà pas si mal !
Enfin, et toujours en relation avec ce troisième point, l’idéal serait pour moi que l’on puisse penser que telle ou telle image ait été réalisée à la main : peinture, crayons, pastel etc.
Les trois contraintes que j’ai retenues impliquent qu’il faut rechercher des équations mathématiques qui n’existent pas “sur étagère” : je suis donc parti de la feuille blanche.
Les équations génériques
Mon travail de recherche des « bonnes équations » a débuté dans les années 2003 – 2004. Pendant ces années j’ai donc commencé par imaginer mes premières équations mais les résultats n’étaient pas au rendez-vous.
Sur un tout autre plan, j’ai eu aussi des difficultés avec la technologie de l’époque qui n’offrait pas encore pour un particulier et à un prix abordable, un ordinateur ayant une puissance de calcul adaptée aux calculs que je programmais.
C’en est suivi des périodes de maturation plus au moins longues, entrecoupées de nouvelles tentatives.
Cet aspect expérimental et un peu austère est à la base de mon parcours.
J’ai découvert – enfin – en 2010-2011 une vingtaine de classes d’équations qui m’ont permis de produire les premières images se rapprochant de ce que je recherchais de manière diffuse.
En voici quelques exemples:

Entrelacs rectangulaires – FLK – 2011

Mobile années cinquante – FLK – 2011

A vous de voir – Up to you – FLK – 2011
Ces équations sont très complexes et n’ont aucun sens scientifique. S’il faut à tout prix leur en donner un, c’est simplement qu’elles permettent de créer des images et c’est cela l’important.
Pour être plus précis, seule une image que je présente sous l’onglet « Singularités » a une « signification mathématique » Elle s’appuie en effet sur une fonction dont la démonstration de certaines de ses propriétés résiste encore aux meilleurs mathématiciens. Les progrès étant très lents, il est vraisemblable que cela demande encore de longues années si l’on pense qu’une démonstration est possible ce qui, en la circonstance, est peut être une hypothèse hardie. Mais il s’agit d’un autre sujet… Revenons à l’image : elle est complètement différente des autres donc vous la trouverez facilement !
Retour au sujet principal …
Les équations que j’ai trouvées, toutes différentes, permettent de créer un vaste ensemble d’images en jouant sur leurs paramètres c’est pourquoi je les nomme « équations génériques » : elles sont à la base de mon travail. C’est le vivier dans lequel je puise pour réaliser d’autres images en particulier les images colorées.
Et, une fois de plus, l’expérimentation est de mise car il est impossible de savoir à l’avance ce que l’on va obtenir. Cela ne signifie pas que les résultats sont aléatoires : ils sont tout simplement absolument imprévisibles ceci à cause de la complexité même des équations.
Il a donc fallu que « j’apprivoise » ces équations pour, par exemple, savoir sur quel(s) paramètre(s) jouer pour obtenir des pleins et des déliés plus ou moins fins.
Voici deux autres exemples pouvant être figuratifs:
La lampe d’Aladin ou l’encensoir en noir et blanc – FLK – 2011

Générique 4 – Aliens entrelacés – FLK – 2011
J’ai ainsi obtenu un grand nombre d’images présentant bien évidemment un intérêt esthétique très variable (à peine quelques pourcents me conviennent). C’est cependant un point de passage incontournable car il faut, pour aboutir à une image qui me plaise, que j’effectue de nombreux essais. Le travail de réglage peut être plus ou moins long selon les équations employées et nécessiter plusieurs jours, voire plus pour les équations les plus « rebelles » et elles sont nombreuses !
![]() Structure des images
Structure des images
La structure des images est très simple : il s’agit en effet d’un ensemble de points reliés les uns aux autres par un trait. Les équations permettent de calculer les coordonnées des points dans l’image.
Les tableaux ci-dessous illustrent les étapes de création d’une image monochrome. Pour plus de clarté les points de l’image sont visualisés par de petits disques rouges.
![]()
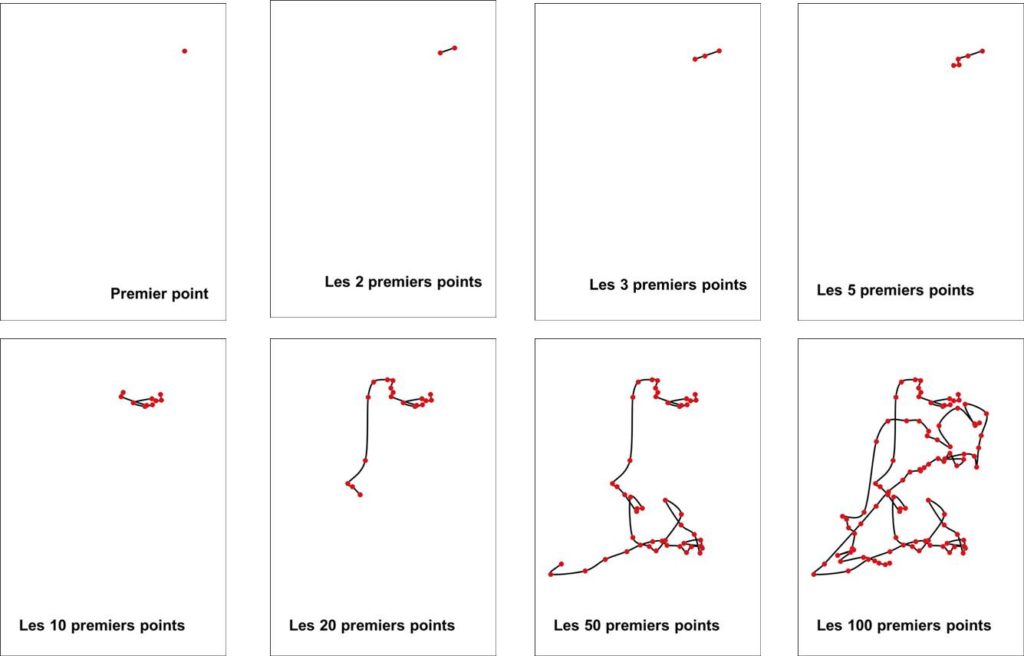
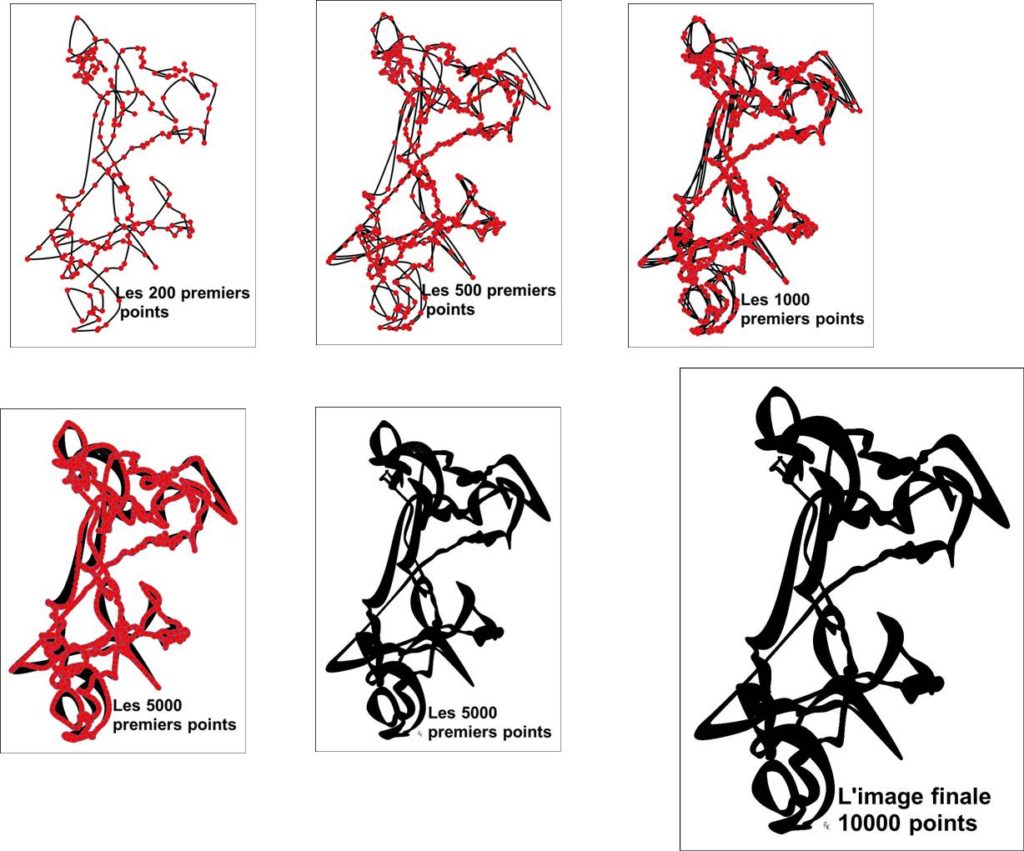
Remarque :
Les différences entre l’image à 5000 points et l’image à 10 000 points n’apparaissent pas dans cette présentation. Mais lors de la mise au point des “trous” apparaissent dans l’image à 5000 points. Cela explique pourquoi 10 000 points sont nécessaires.
Une caractéristique de ces images est que, par exemple, le point le plus proche du point P1 n’est pratiquement jamais le point P2 (le point suivant dans la liste) mais, au terme des calculs, disons le point P1515 lorsque l’on est (militairement) optimiste ou le point P1815 lorsqu’on l’est moins.
Dans le tableau ci-dessus il est clair que le point P2 n’est pas le point le plus proche de P1; le plus proche est le point P… je ne sais pas lequel!!! On peut évidemment obtenir son numéro en recherchant le point le plus proche de P1 dans la liste des points définissant l’image mais cela n’a pas vraiment d’intérêt; du moins jusqu’à aujourd’hui.
Une conséquence de la structure de l’image est que l’introduction simple de la couleur est en pratique impossible. Il faut donc contourner le problème.
L’introduction de la couleur

Ce travail a débuté en 2012-2013. La solution que j’ai retenue est d’appliquer à une image monochrome, une succession de transformations mathématiques et, pour chaque nouvelle image ainsi obtenue, d’en changer la couleur et de superposer les images les unes après les autres.
Contexte clinique !!!
Dans mon travail, les couleurs que j’emploie principalement sont :
– l’ocre, le jaune, le bleu, le rouge et le noir,
– 5 dégradés de bleu,
– un mélange de toutes les couleurs précédentes,
– et, un peu moins toutefois, la couleur verte.
Ces couleurs sont les miennes dans le sens où ces couleurs me permettent de travailler : il s’agit d’une espèce de signature chromatique. Ce choix est dû au fait que je suis daltonien.
Voici un exemple illustratif du daltonisme : dans l’image ci-dessous une vision normale voit un « 6 » et moi rien du tout !

Image extraite de l’article de Wikipédia consacré au daltonisme (test de d’Ishihara) Pour plus d’information rendez-vous à l’adresse suivante: https://fr.wikipedia.org/wiki/Daltonisme
Le daltonisme n’est pas un handicap au contraire : je peux faire des images qui me plaisent en accolant telles ou telles couleurs et aboutir ainsi à une image pouvant surprendre une personne à la vision ” normale “. Cet aspect peut ainsi rendre mes images encore plus originales !
Les paramètres définissant les couleurs étant des paramètres comme les autres, ils peuvent être modifiés selon vos désirs. On peut ainsi aboutir à une œuvre unique : je calcule les points et je prends vos couleurs en compte pour former l’image finale. Pour plus de détail sur la gestion des couleurs suivez le lien Informations pratiques .
FLK
![]()
J’appelle l’image monochrome de départ « image source » car les images colorées auxquelles j’aboutis ne pourraient exister sans elle.
Il y a donc une filiation ou des « gènes communs » entre cette image et les images colorées que j’appelle en conséquence « images avatars »
Une “image source” est représentée ci-dessous.
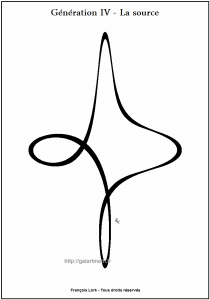
Génération IV – La source Courbe douce – Smooth curve – FLK – 2011
Si on doit calculer les positions de N points pour former l’image source il faudra donc calculer 5 fois ce nombre pour obtenir des images contenant 5 images colorées d’où l’absolue nécessité d’avoir un moyen de calcul suffisamment puissant pour réduire la durée des calculs.
Pour fixer les idées : si l’image source nécessite de calculer les coordonnées de 20 000 points (ce qui est très souvent le cas pour aboutir à une image nette) l’image finale avec 5 couleurs en contiendra 100 000 (superposition de 5 images de 20 000 points) On doit donc calculer 200 000 nombres : 2 nombres sont en effet nécessaires pour définir la position d’un point dans l’image.
Dans ce contexte les tables numériques, la règle à calcul et la calculette ne sont d’aucun secours ! Il est donc nécessaire d’utiliser un ordinateur.
Les images ci-après illustrent l’introduction de la couleur.

Génération IV – Courbes douces en noir et bleu – Smooth dark and blue curves – FLK – 2015
L’image bleue a été obtenue en appliquant à l’images noire d’origine une symétrie par rapport à l’axe vertical et bien sûr en la colorant en bleu !
FLK
Voici un second exemple :

Dégradé de bleu évoquant des fonds marins – FLK – 2015

Fonds marins multicolores – FLK – 2015
Ces deux images colorées – qui sont un détail de l’image globale obtenue au terme des transformations – ont été “construites” à partir de l’image source présentée plus haut. Ici cinq transformations ont été appliquées à l’image source d’où les cinq couleurs.
Les deux images ont donc exactement les mêmes points dont les positions ont été obtenues par calcul. Dans l’image de gauche on peut y voir des “algues bleues” L’image de droite peut faire songer à des fonds marins colorés mais où ?
FLK
Voici une seconde image bicolore. La nature mathématique de l’image apparaît peu ou prou mais je ne la rejette pas et ce, même si je suis en contradiction avec la troisième contrainte que je me suis fixée…

Image noire et bleue I – Black and blue curves – FLK – 2015
A ce stade, on peut remarquer qu’il est possible de modifier la perception des images polychromes en :
- changeant tout simplement les couleurs (choisir par exemple des dégradés de bleu)
- modifiant l’ordre d’apparition des couleurs,
- modifiant l’ordre d’apparition des images.
- « mélangeant » un peu de tout ce qui précède.
C’est ce que je fais parfois, notamment avec des images présentant une symétrie axiale ou une symétrie par rapport à un point : cette façon de procéder « gomme » la symétrie de l’image initiale. J’appelle donc ces images des « images caméléon » : la symétrie mathématique est toujours présente mais n’apparaît plus de manière aussi évidente. Il faut remarquer que réaliser de telles images demande beaucoup de travail.
En voici un exemple :

Image caméléon 1 – FLK – 2015
D’autres images de ce type sont présentées dans ce site (voir l’onglet “Générations” et l’onglet « Singularités ») : à vous de les découvrir !
![]()
Dans ma quête d’images qui me plaisent (*) j’ai été amené à imaginer un second ensemble d’équations que j’applique aux “images source” Ces équations sont assez tordues d’un point de vue mathématique mais on s’en moque ! L’emploi d’un ordinateur permet de tester facilement beaucoup d’équations et d’ouvrir ainsi de nouveaux horizons.
(*) On pourrait dire images « nouvelles » ou « originales » mais la nouveauté ou l’originalité ne sont pas ce qui me guident : je cherche simplement des images qui me plaisent.
Il faut remarquer que l’application d’une de ces équations à une image source peut donner de « bons résultats » tandis que, pour une autre image source, et en lui appliquant les mêmes équations, le résultat sera décevant (voire carrément laid) Une fois de plus il faut expérimenter encore et encore.
![]()


Compléments et synthèse
En résumé, j’ai construit de toute pièce une boîte à outils (que je continue à faire vivre selon l’inspiration du moment) constituée des éléments suivants :
- Une vingtaine d’équations génériques dotées chacune de leurs propres paramètres sur lesquels on peut jouer,
- Plus de
250(250 c’était en avril 2016) 300 équations permettant de transformer une image (pour être précis 320 au début mai 2017. Je suis en train de les explorer), - Un ensemble de transformations « exotiques » issues de mon imagination.
- Un ensemble de transformations géométriques classiques : rotation, translation, facteur d’échelle etc. Donc ici l’imagination n’est évidemment pas présente : il suffit en effet de les programmer (comme tout logiciel sans faire de fautes et éviter les redoutables divisions par zéro ou les non moins redoutables boucles infinies ! ),
La créativité « mathématico artistique » ne concerne que les points 1, 2 et 3 et je me sers en tant que de besoin des transformations du quatrième point.
Pour travailler sur une image j’ai ainsi tout cela face à moi sur l’écran de mon ordinateur ce qui est la pure vérité.
J’ai en effet dû créer une interface me permettant d’expérimenter facilement. On y trouve le numéro des équations génériques, les valeurs choisies pour le paramétrage, le numéro des transformations choisies, le choix de couleurs etc.
Après de nombreuses expérimentations qui sont – une fois de plus – nécessaires pour appréhender le comportement de tel ou tel paramétrage, la démarche artistique à proprement parler consiste alors à mettre en œuvre tout ou partie de ces outils pour créer des images qui me plaisent et qui, je l’espère, vous plairont également.
![]()
Ce travail est un travail itératif du type essai/sélection :
- Quel paramétrage choisir et pour quel(s) effet(s) souhaité(s) ?
- Quelles transformations appliquer ?
- Quelles couleurs choisir et dans quel ordre ?
- Que faire pour donner un effet de perspective à l’image?
- Doit-on conserver ou non une symétrie ?
- Et si je faisais ça? Ou bien ça ?…
Ce travail de mise au point est vraiment l’étape la plus importante et la plus excitante car c’est au cours de celle-ci que la création artistique s’exprime. Il s’agit alors de rechercher comment assembler tous ces éléments pour en faire une “bonne” image.
Il faut noter que j’ai longuement tenté d’apprivoiser toutes les équations que je manipule et que, malgré cela, je continue d’être parfois très surpris par les résultats obtenus.
On pourrait être tenté de croire que l’on peut prendre des réglages et choisir des équations de façon aléatoire tant l’explosion combinatoire est implicitement présente.
Ceci est cependant voué à l’échec (sauf coup de chance très improbable) car il y a un lien – de nature insaisissable – entre certaines combinaisons d’équations, de paramètres, de transformation etc. Le travail d’expérimentation consiste entre autre à cerner les bonnes ou les mauvaises combinaisons d’équations. Il s’agit donc toujours d’un processus expérimental d’essai/sélection ce qui allonge le temps de mise au point d’une image.
![]()
Perspectives – utilisation des images
Et enfin : que peut-on faire de ces images ?
Les images se suffisent à elles-mêmes et peuvent être encadrées (ou non) et exposées.
Mais après réflexion et différents essais, je pense que l’on pourrait utiliser certaines images comme modèle pour réaliser :
- des vitraux,
- des fresques,
- des tapis,
- du carrelage,
- du papier peint,
- des décors de plats, d’assiettes etc.
- …
Voici pour illustrer mon propos deux exemples qui pourraient servir de motif pour créer des assiettes, en porcelaine de préférence, car j’aime beaucoup ce type d’objet et notamment les porcelaines dites “de la Compagnie des Indes”


Si le visiteur est arrivé jusqu’ici merci de me faire part de vos éventuels commentaires, demandes d’éclaircissement ou tout autre point (voir onglet « Contact »)
François Lork – mai 2017